Analytical solution of the Pennes equation in time-domain for one-dimension

Jan 30, 2017 by Hugo Milan

You can download the algorithm D1_BHE_f.m for Octave/Matlab that can solve this problem here and you can see instructions in how to use it here. If you want to see the final solution, go to Solution.

In this page, we will solve the dynamic Pennes equation in one-dimension using the principles of superposition and separation of variables. The problem we will solve is restricted to the following initial and boundary conditions:

$\begin{matrix} T(y, t = 0) = T_{c}\\ T(y = 0, t) = T_{c}\\ T(y = H, t) = T_{s} \end{matrix}$

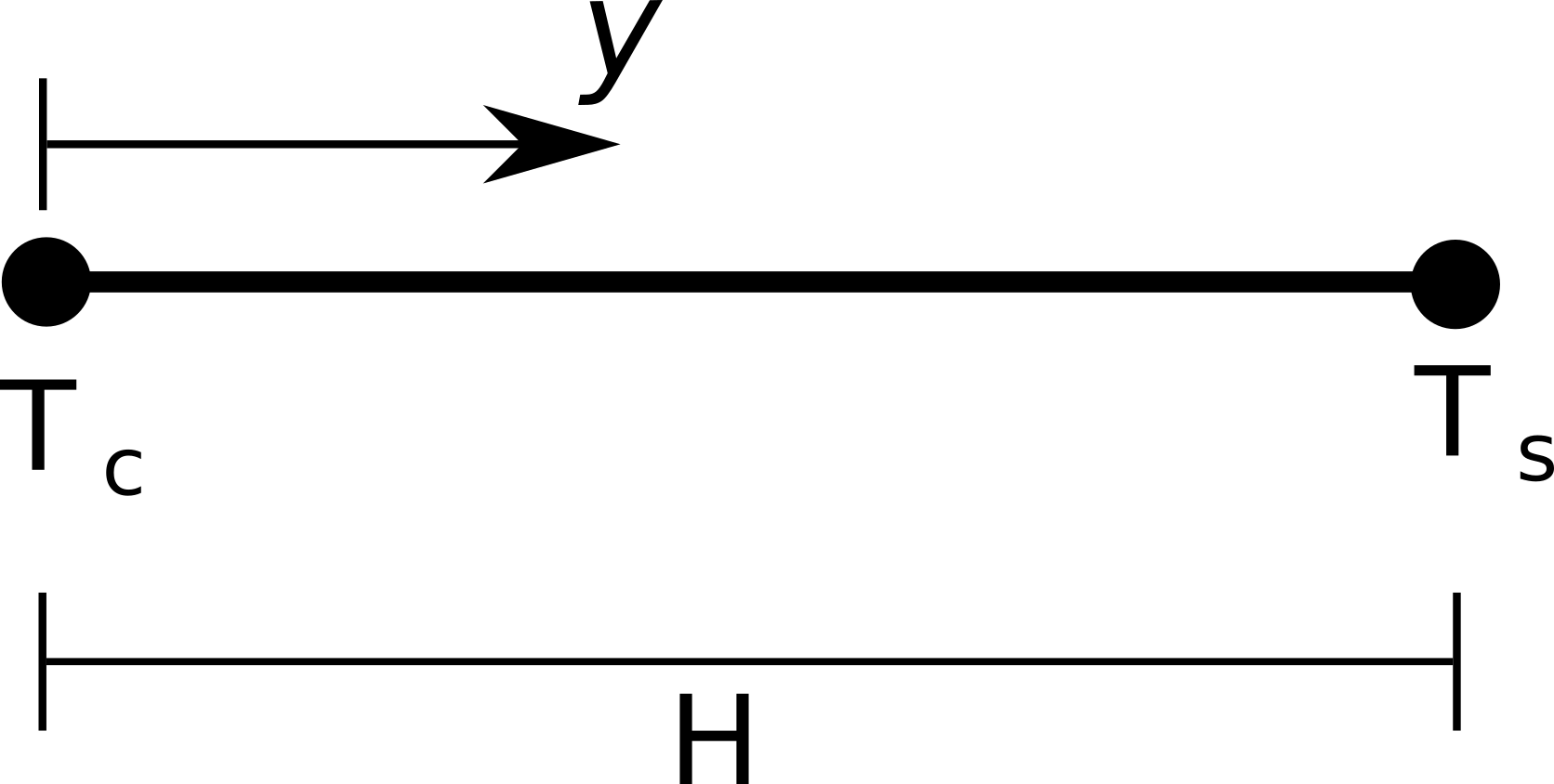
The problem geometry for the pennes equation can be represented as shown below. Geometry of the one-dimensional problem for Pennes equation

Governing equations

The Pennes equation is defined as:

\begin{equation} \rho c_{p}\frac{\partial T}{\partial t} = k\frac{\partial^2 T}{\partial y^2} + S + Q_m + \omega_b\rho_b c_{b} (T_b - T) \label{eq:Pennes} \end{equation}

where $T$ is temperature, $t$ is time, $\rho$ is density, $c_{p}$ is specific heat, $k$ is heat conductivity, and $S$ is source, $Q_m$ is metabolic heat generation, $\omega_b$ is blood perfusion, $\rho_b$ is blodd density, $c_{b}$ is blood specific heat, and $T_b$ is blood temperature.

Solving

I will use the principle of suporposition so that:

\begin{equation} T(y,t) = T_c + \phi_a(y) + \phi_b(y)\tau_b(t) \label{eq:Sup} \end{equation}

and the initial and boundary conditions for these problems are:

$\begin{matrix} & T(y,t) & \phi_a(y) & \phi_b(y)\tau_b(t) \\ t = 0 & T = T_c & - & \phi_b\tau_b = -\phi_a\\ y = 0 & T = T_c & \phi_a = 0 & \phi_b\tau_b = 0\\ y = H & T = T_s & \phi_a = T_s - T_c & \phi_b\tau_b = 0 \end{matrix}$

Defining $W_b = \omega_b\rho_b c_{b} $ and applying Eq. \ref{eq:Sup} in \ref{eq:Pennes} yields

\begin{equation} k\frac{\partial^2 \phi_a}{\partial y^2} - W_b\phi_a + S + Q_m + W_b(T_b - T_c) = \rho c_{p}\phi_b\frac{\partial \tau_b}{\partial t} - k\tau_b\frac{\partial^2 \phi_b}{\partial y^2} + W_b\phi_b\tau_b = 0 \end{equation}

which implies that we can solve Eqs. \ref{eq:a} and \ref{eq:b} \begin{equation} k\frac{\partial^2 \phi_a}{\partial y^2} - W_b\phi_a + S + Q_m + W_b(T_b - T_c) = 0 \label{eq:a} \end{equation}

\begin{equation} \rho c_{p}\phi_b\frac{\partial \tau_b}{\partial t} - k\tau_b\frac{\partial^2 \phi_b}{\partial y^2} + W_b\phi_b\tau_b = 0 \label{eq:b} \end{equation}

Solving Eq. \ref{eq:a}

Defining

\begin{equation} Q_t = S + Q_m + W_b(T_b - T_c) \end{equation}

the general solution of Eq. \ref{eq:a} is

\begin{equation} \phi_a = \frac{Q_t}{W_b} + c_1 \sinh{ \left( y\sqrt{\dfrac{W_b}{k}} \right) } + c_2\cosh{ \left( y\sqrt{\dfrac{W_b}{k}} \right) } \end{equation}

Applying the boundary condition at $y = 0$

\begin{equation} c_2 = -\dfrac{Q_t}{W_b} \end{equation}

Applying the boundary condition at $y=H$ we get: \begin{equation} c_1 = \frac{\left( T_s - T_c \right) + \dfrac{Q_t}{W_b}\left[ \cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right) } - 1\right]}{\sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right) }} \end{equation}

So, the final solution for $\phi_a$ is:

\begin{equation} \phi_a = \frac{Q_t}{W_b} + \left\{ \left( T_s - T_c \right) + \dfrac{Q_t}{W_b}\left[ \cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right) } - 1\right] \right\}\frac{\sinh{ \left( y\sqrt{\dfrac{W_b}{k}} \right)}}{\sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right) }} \ldots\\ \ldots - \frac{Q_t}{W_b} \cosh{ \left( y\sqrt{\dfrac{W_b}{k}} \right) } \end{equation}

Note that this solution is not suitable for $W_b = 0$. In this case, the correct solution is for the heat equation shown here.

Solving Eq. \ref{eq:b}

We will use separation of variables to solve Eq. \ref{eq:b}. In separation of variables, we assume that the solution is the multiplication of a function of $y$ ( $\phi_b(y)$ ) and $t$ ( $\tau_b(t)$ ). Hence,

\begin{equation} \frac{\rho c_{p}}{k\tau_b}\frac{\partial \tau_b}{\partial t} + \frac{W_b}{k} = \frac{1}{\phi_b}\frac{\partial^2 \phi_b}{\partial y^2} = -\lambda_m^2 \end{equation}

The solution of $\phi_b$ can be expressed as:

\begin{equation} \phi_b = c_3 \sin{\left(\lambda_m y\right)} + c_4 \cos{\left(\lambda_m y\right)} \end{equation}

Applying the boundary condition at $y = 0$ we get $c_4 = 0$. Applying the boundary condition at $y=H$ we get:

\begin{equation} \sin{\left(\lambda_m H\right)} = 0 \label{eq:lambdam} \end{equation}

which implies that

\begin{equation} \lambda_m = \frac{m\pi}{H} \end{equation}

with $m = 1, 2, 3, \dotsc$ We start the counting from $1$ because $m = 0$ yields $\phi_b = 0$. Now, defining $\alpha = k/(\rho c_p) $, the solution of $\tau_b$ is:

\begin{equation} \tau_b = c_5 \exp{\left[-\alpha t \left(\lambda_m^2 + \dfrac{W_b}{k} \right)\right]} \end{equation}

Therefore, the solution that we are looking for is:

\begin{equation} \phi_b\tau_b = \sum_{m=1}^{\infty}c_m \sin{\left(\lambda_m y\right)} \exp{\left[-\alpha t \left(\lambda_m^2 + \dfrac{W_b}{k} \right)\right]} \label{eq:b:almost} \end{equation}

Now, we apply the initial condition and get

\begin{equation} \sum_{m=1}^{\infty}c_m \sin{\left(\lambda_m y\right)} = -\phi_a \label{eq:b:cm} \end{equation}

To solve Eq. \ref{eq:b:cm}, we multiply both sides by an orthogonal function of the function that multiplies $c_m$ and integrate it from $y = 0$ to $y = H$ to elimate the $y$ dependence. That is, we need a function that is orthogonal to $\sin{\left(\lambda_m y\right)}$. The function that we are looking for is $\sin{\left(\lambda_n y\right)}$. Multiplying both sides by this function yields

\begin{equation} \int_{y=0}^{y=H}\sum_{m=1}^{\infty}c_m \sin{\left(\lambda_m y\right)}\sin{\left(\lambda_n y\right)} dy = - \int_{y=0}^{y=H}\phi_a\sin{\left(\lambda_n y\right)} dy \label{eq:b:cm2} \end{equation}

Since we have

\begin{equation} \int_{y=0}^{y=H} \sin{\left(\lambda_m y\right)}\sin{\left(\lambda_n y\right)} dy = 0 \end{equation}

for $m \neq n$, and

\begin{equation} \int_{y=0}^{y=H} \sin{\left(\lambda_m y\right)}\sin{\left(\lambda_n y\right)} dy = \frac{H}{2} \label{eq:mn} \end{equation}

for $m = n$, we can drop the summation and solve Eq. \ref{eq:b:cm2} for each $c_m$:

\begin{equation} c_m = - \dfrac{\displaystyle \int_{y=0}^{y=H}\phi_a\sin{\left(\lambda_n y\right)} dy}{ \displaystyle \int_{y=0}^{y=H}\sin^2{\left(\lambda_m y\right)} dy } \label{eq:b:cm3} \end{equation}

The solutions of these integrals are:

\begin{equation} -\frac{Q_t}{W_b} \int_{y=0}^{y=H} \sin{\left(\lambda_n y\right)} dy = \frac{Q_t}{W_b\lambda_m}\left[\cos{ \left( \lambda_m H\right) } - 1 \right] \end{equation}

From the definition of $\lambda_m$ in Eq. \ref{eq:lambdam},

\begin{equation} -\frac{Q_t}{W_b} \int_{y=0}^{y=H} \sin{\left(\lambda_n y\right)} dy = \frac{Q_t}{W_b\lambda_m}\left[\left( -1 \right)^m - 1 \right] \end{equation}

The next integral,

\begin{equation} -c_1 \int_{y=0}^{y=H} \sinh{ \left( y\sqrt{\dfrac{W_b}{k}} \right)} \sin{\left(\lambda_n y\right)} dy = \ldots \\ \ldots c_1 \frac{\lambda_m\sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} \cos{\left(\lambda_n H\right)} - \sqrt{\dfrac{W_b}{k}} \cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} \sin{\left(\lambda_n H\right)} }{ \dfrac{W_b}{k} + \lambda_m^2} \end{equation}

From the definition of $\lambda_m$ in Eq. \ref{eq:lambdam},

\begin{equation} -c_1 \int_{y=0}^{y=H} \sinh{ \left( y\sqrt{\dfrac{W_b}{k}} \right)} \sin{\left(\lambda_n y\right)} dy = \left( -1 \right)^m c_1 \frac{\lambda_m\sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} }{ \dfrac{W_b}{k} + \lambda_m^2} \end{equation}

And the last integral,

\begin{equation} \frac{Q_t}{W_b} \int_{y=0}^{y=H} \cosh{ \left( y\sqrt{\dfrac{W_b}{k}} \right) } \sin{\left(\lambda_n y\right)} dy = \ldots \\ \ldots \frac{Q_t}{W_b} \frac{ \sqrt{\dfrac{W_b}{k}} \sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} \sin{\left(\lambda_n H\right)} - \lambda_m\cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} \cos{\left(\lambda_n H\right)} + \lambda_m }{ \dfrac{W_b}{k} + \lambda_m^2} \end{equation}

which, from the definition of $\lambda_m$ in Eq. \ref{eq:lambdam}, becomes

\begin{equation} \frac{Q_t}{W_b} \int_{y=0}^{y=H} \cosh{ \left( y\sqrt{\dfrac{W_b}{k}} \right) } \sin{\left(\lambda_n y\right)} dy = \frac{Q_t\lambda_m}{W_b} \frac{ 1 - \left( -1 \right)^m\cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} }{ \dfrac{W_b}{k} + \lambda_m^2} \end{equation}

Defining,

\begin{eqnarray} c_m &=& c_{m1} + c_{m2} + c_{m3}\\ c_{m1} &=& \frac{2Q_t}{HW_b\lambda_m}\left[\left( -1 \right)^m - 1 \right]\\ c_{m2} &=& \left( -1 \right)^m \frac{2\lambda_m c_1}{H} \frac{\sinh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} }{ \dfrac{W_b}{k} + \lambda_m^2}\\ c_{m3} &=& \frac{2Q_t\lambda_m}{HW_b} \frac{ 1 - \left( -1 \right)^m\cosh{ \left( H\sqrt{\dfrac{W_b}{k}} \right)} }{ \dfrac{W_b}{k} + \lambda_m^2} \end{eqnarray}

The final solution is, simply,

\begin{equation} \phi_b\tau_b = \sum_{m=1}^{\infty}c_m \sin{\left(\lambda_m y\right)} \exp{\left[-\alpha t \left(\lambda_m^2 + \dfrac{W_b}{k} \right)\right]} \label{eq:b:final} \end{equation}

Note that this solution is not suitable for $W_b = 0$. In this case, the correct solution is for the heat equation shown here.

Solution

The final solution is:

\begin{equation} T(y,t) = T_c + \phi_a(y) + \phi_b(y)\tau_b(t) \end{equation}

with $\alpha = k/( \rho c_p ) $, and $\phi_a(y)$ and $\phi_b(y)\tau_b(t)$ expressed as:

\begin{equation} \lambda_m = \frac{m\pi}{H} \end{equation}

\begin{equation} \phi_b\tau_b = \sum_{m=1}^{\infty}c_m \sin{\left(\lambda_m y\right)} \exp{\left[-\alpha t \left(\lambda_m^2 + \dfrac{W_b}{k} \right)\right]} \end{equation}

The heat flux can be obtained by derivating these equations with respect to $y$.

Note that this solution is not suitable for $W_b = 0$. In this case, the correct solution is for the heat equation shown here.

Using the Algorithm

The algorithm D1_BHE_f.m was written as a function in Octave/Matlab and you can obtain it here. To use it, you will need to define the material properties and the maximum value of $m$.

As an example, we can use the following script:

% Thermal properties
Tc = 37; % core and initial temperature (oC)
Ts = 150; % superficial temperature (oC)
rho = 1200; % tissue density (kg/m3)
cp = 3200; % specific heat (J/(K-kg))
k = 0.3; % thermal conductivity (W/(K-m))
wb = 1e-4; % blood perfusion (s-1)
rhob = 1052; % blood density (kg/m3)
cb = 3600; % blood specific heat (J/(K-kg))
Tb = 37; % temperature of the blood (oC)

Qmet = 500; % internal heat generation (W/m3)
% If there is another heat source S besides Qmet, sum it to Qmet.
% For example, if Qmet = 250 and S = 250, you would input Qmet = 500.
    
% Material properties
H = 1e-3; % m
y = 0:(H/100):H;
    
% number of iterations of m
minf = 50;
    
% time of the solution
t = 0.5;
    
[T, q] = D1_BHE_f(y, H, t, Ts, Tc, k, rho, cp, wb, rhob, cb, Tb, Qmet, minf);
    
plot(y, T)
    
figure;
    
plot(y, q)

which generates

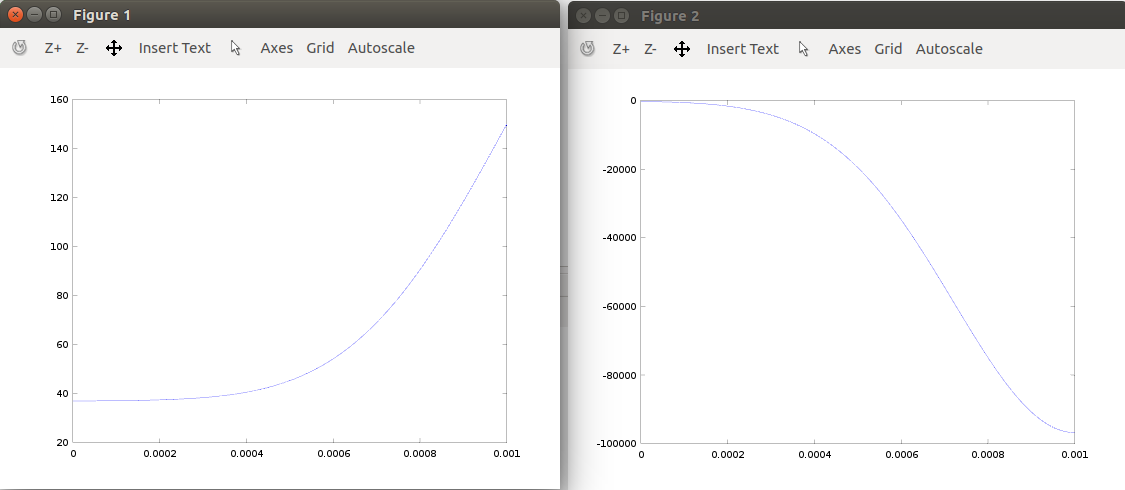
Solution of the problem for Pennes equation

Limitations

Every solution method has limitations. The most noticeable limitation is that we have to perform infinity sums to get predictions using solutions from separation of variables. Infinity sums, however, cannot be performed in numerical computations, which leads us to truncate the calculations for large values of $m$. How large this number have to be will depend on the problem geometry and on the material properties but, if theses number are not large enough, the calculations will manifest oscillations that will be most evident for predicted fluxes. When observed that $m$ has to be increased, a rule-of-thumb is to double its valuee, re-calculate the predicionts, and observe if the oscillations have decreased to acceptable intensities.

Done

Now, you can go to: